More On 1,2 and 1,4 Additions To Dienes

Two More Diene Reactions: Free-Radical Addition of HBr to Dienes, and Addition of Br₂ to Dienes

In an earlier post we covered 1,2 and 1,4 additions to dienes, specifically the addition of strong acid (e.g. HCl or HBr) to dienes.

You might rightfully ask, “is that it?”. Are there any other examples of reactions that give “1,2” vs “1,4” products?

Why yes, thank you for asking. Today we’ll go through two more: free-radical addition of HBr to dienes, and the addition of Br₂ to dienes.
Oh, and we’ll also work through three 1,2- versus 1,4- addition product practice problems.

Table of Contents

1. Recap: “1,2” vs. “1,4” Addition To Dienes, And “Kinetic Control” vs “Thermodynamic Control “
2. Free-Radical Addition of HBr to Dienes Is Also Subject To Kinetic And Thermodynamic Control
3. In Radical Addition Of HBr To Butadiene, The 1,2- Product Is The Kinetic Product And The 1,4- Product Is The Thermodynamic Product
4. Addition of Br₂ (And Other Halogens) to Dienes
5. 1,2- And 1,4- Products In Addition Of Br₂ To Butadiene
6. The Role Of Temperature In Determining The Product Ratio Of 1,2- And 1,4- Addition Of Br₂ To Butadiene
7. A Different Rationalization For Why The 1,2- Product Is The Kinetic Product: Ion Pairing
8. Thinking Through “Kinetic” and “Thermodynamic” Control – Three Practice Problems
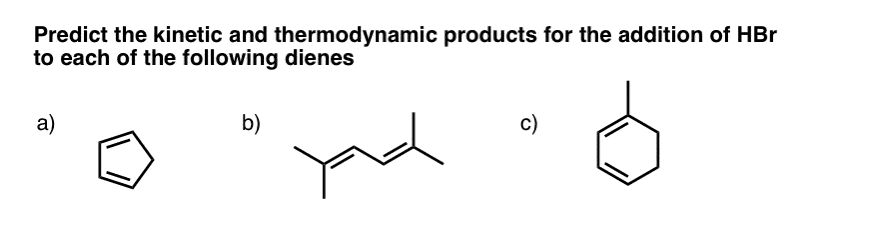
9. Question #1. Cyclopentadiene
10. Question #2 (2,5 dimethyl hexa-2-4-diene)
11. Question #3: 1-Methyl Cyclohexadiene
12. Conclusion
13. Notes
14. (Advanced) References and Further Reading

1. Recap: “1,2” vs. “1,4” Addition To Dienes, And “Kinetic Control” vs “Thermodynamic Control”

To recap: In Org 1 we learned that addition of HCl and HBr to normal, isolated alkenes (such as 1-butene) just gives one product – the Markvonikoff product (“1,2-addition”) where the H and the nucleophile (e.g. Br-) are on adjacent carbons, and Br has added to the most substituted carbon.

However, addition of acid to a diene results in a resonance-stabilized carbocation, which can undergo attack by the nucleophile at two possible positions, and thus can lead to two different products.

The two different products are the “1,2-addition” product, where the H and Br are on adjacent carbons, and the “1,4-addition” product, where the carbons bearing H and Br are separated by a double bond.

Temperature plays a key role in determining the product distribution. At low temperatures, the reaction is irreversible and the product that proceeds through the lowest-energy transition state (i.e. the product that is formed fastest!)  is favoured. We rationalized this by saying that attack occurred at the carbon best able to stabilize positive charge (i.e the “resonance form” with the most stable carbocation). At higher temperatures, the reaction becomes reversible, and the favoured product will be the one with the most substituted double bond (not unlike Zaitsev’s Rule)  We call these two conditions, respectively, kinetic control  and thermodynamic control.

We finished up the post with a quiz, which I’m reproducing here.

We’ll dig into the answers for these questions at the bottom.

But first, for completeness, let’s cover two other reactions of dienes that can lead to 1,2- and 1,4- addition products.

• Addition of HBr to dienes under free-radical conditions
• Addition of Br₂ (and other dihalogens such as Cl₂ and I₂) to dienes.

It’s quite possible you may never see these reactions of dienes in your course. So you can think of this as a bonus topic.

2. Free-Radical Addition of HBr to Dienes Is Also Subject To Kinetic And Thermodynamic Control

You may recall that addition of HBr to dienes under free-radical conditions follows a different reaction pathway than that of plain-vanilla addition of HBr. Specifically, heating HBr in the presence of a free-radical initiator (such as di t-butyl peroxide, benzoyl peroxide, AIBN, or just “peroxides”) results in formation of the bromine radical Br• , which adds to alkenes in such a way as to favor the most stable radical intermediate. [See Post: Free Radical Addition]

In practice, this results in “anti-Markovnikov” addition to an alkene, where Br• adds to the least substituted carbon of the double bond, and the radical ends up on the most substituted (and therefore most stable) carbon.

When Br• adds to a diene, we obtain a resonance-stabilized free radical. This radical will have two important resonance forms, and two products can potentially form, depending on whether the radical abstracts a hydrogen from H–Br at C-2 or C-4.

Below, we’ve drawn what this looks like in the addition of Br• to butadiene.  (For brevity, we’ve skipped writing out the mechanism and the radical initiation step,  but it’s covered in the post referenced above if you need a refresher.)

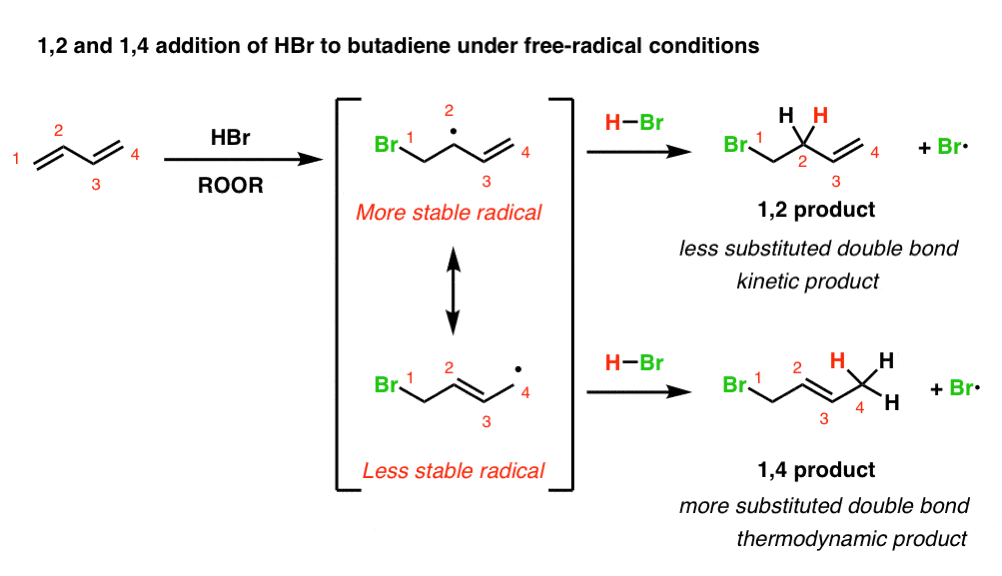
(obligatory reminder:  resonance forms are not in equilibrium. they just make different contributions to the resonance hybrid)

3. In Radical Addition Of HBr To Butadiene, The 1,2- Product Is The Kinetic Product And The 1,4- Product Is The Thermodynamic Product

Note that attack of Br• at C-1 of butadiene leads to a pair of resonance forms not unlike the resonance forms we saw in addition of HBr under non-radical conditions. Like carbocations, free radicals increase in stability as the number of attached carbons increases.

We should therefore expect the top resonance form (where the radical is on a secondary carbon, C-2) to be the dominant contributor to the resonance hybrid, and the bottom resonance form (where the radical is on a primary carbon,  C-4) to be the minor contributor to the resonance hybrid.

[Why does Br• attack C-1 (or C-4, since butadiene is symmetrical)? Because that will generate a (stabilized) allylic free radical. Attack at C-2 or C-3 does not give a resonance-stabilized free radical and is therefore less favoured ]

Since the 1,2- product is formed through a lower-energy (i.e. more stable) transition state, we might expect it to always be the major product. And indeed, at low temperatures, where the reaction is irreversible, this is the case.

However, you might recall from Zaitsev’s rule that the thermodynamic stability of alkenes increases as  C-H bonds on the alkene are swapped for C-C bonds. Hence the 1,4 product (a di-substituted alkene) is more thermodynamically stable than the 1,2-product (a mono-substituted alkene).

At higher temperatures, where the reaction becomes reversible, we would thus expect the 1,4-product to dominate.

This would appear to set up a situation like that for addition of HBr to dienes under non-radical conditions, where we have a kinetic (1,2) product and a thermodynamic (1,4) product, and can thus control the product distribution with heat. In practice, however, it is hard to observe “pure” radical addition without interference from the carbocation pathway, especially at higher temperatures.

4.  Addition of Br₂ (And Other Halogens) to Dienes

Another family of electrophiles that can perform 1,4 addition to dienes is dihalogens such as Cl₂, Br₂, and I₂.

You may recall from Org 1 that dihalogens add to alkenes to generate 1,2 dihalides (also known as “vicinal” dihalides) and this reaction proceeds through a charged, 3-membered ring intermediate (e.g. a “bromonium ion”). This 3-membered ring intermediate is generally quite stable, as evidenced by the fact that the stereochemistry of the addition is generally anti. [If a free carbocation were present, we’d get mixtures of syn and anti, since the carbocation is flat and can accept nucleophiles from two directions].

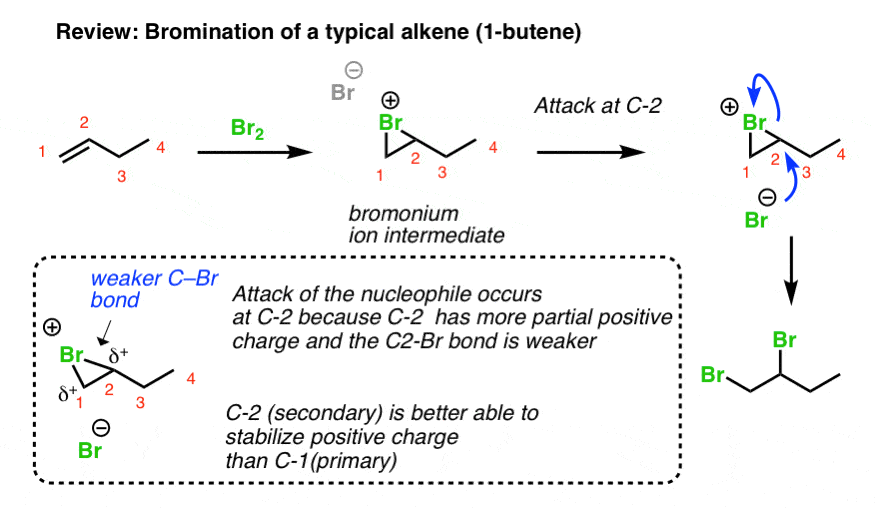
You can think of the second step of this process (attack of Br-) as being a hybrid of the S_N1 and S_N2 reactions. Like the S_N1 reaction, attack is favoured at the carbon best able to stabilize positive charge (generally, the most substituted carbocation). Like the S_N2 reaction (and unlike the S_N1), attack occurs with inversion of configuration.

5. 1,2- And 1,4- Products In Addition Of Br₂ To Butadiene

When a dihalogen such as Br₂ is added to a diene such as butadiene, a bromonium ion intermediate will form on one of the double bonds. Attack of the nucleophile can occur at two different positions. Attack at C-2 provides the 1,2-product. Attack at C-4 provides the 1,4-product.

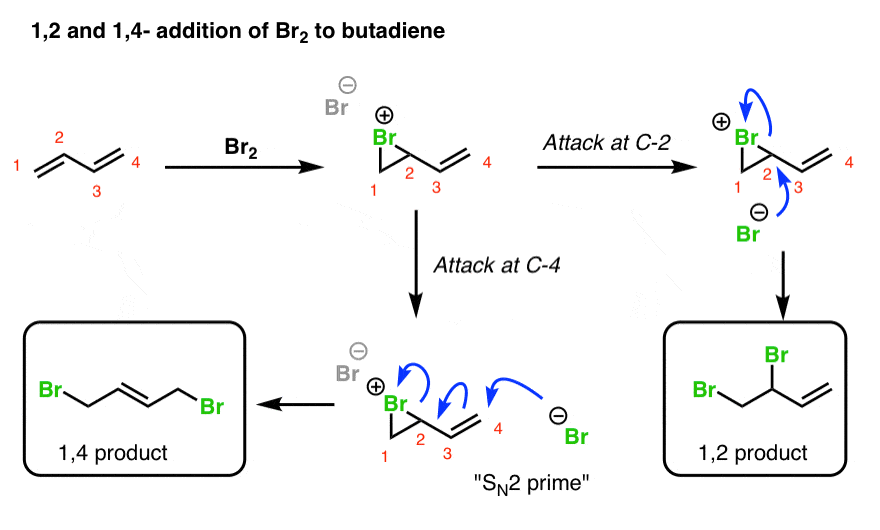
Wait! you might well ask. How does this work? C-4 doesn’t even have a leaving group!!

True!  However, there is a good leaving group on C-2 (the Br), and there is a pi bond between C-3 and C-4. So you can imagine the following chain of events occurring:

• The Br(-) attacks C-4, forming C-Br,
• … resulting in breakage of the pi bond between C-3 and C-4 and formation of a new pi bond between C-2 and C-3,
• … which displaces the leaving group on C-2

In other words it may be helpful to think of that intermediate double bond as a nucleophile that “pushes out” the Br leaving group on C-2.

This process is reminiscent of the S_N2 reaction, except that a double bond intervenes between the nucleophile and the leaving group. For this reason this type of reaction is often called an S_N2′  reaction (“SN2 prime”). It doesn’t appear all that much in introductory organic chemistry courses, but when it does come up… it tends to be on exams!

So which product is favoured?

6. The Role Of Temperature In Determining The Product Ratio Of 1,2- And 1,4- Addition Of Br₂ To Butadiene

Let’s look at the results when temperature is varied.

• At low temperatures, 1,2-addition to butadiene is dominant (60:40 at –15°C).
• At higher temperatures, the 1,4- product is major (90:10 at 60°C).

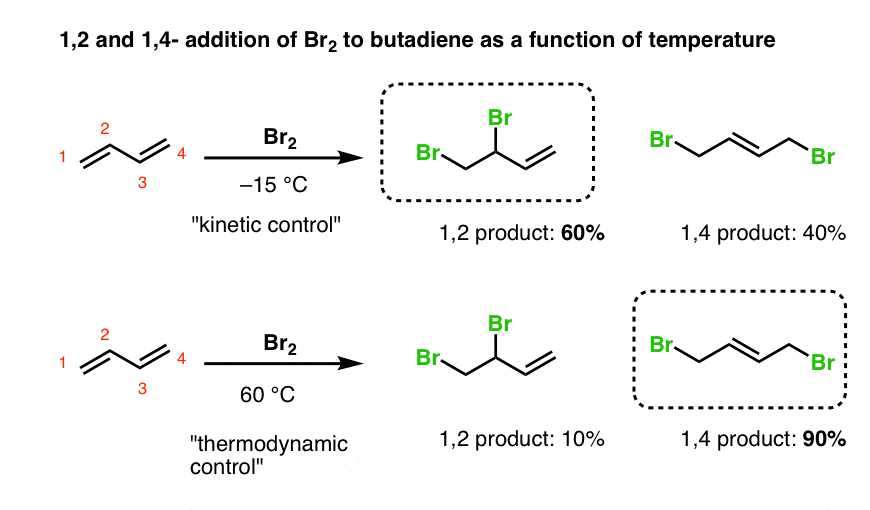
With butadiene, we again have a situation where the “1,2-addition” product is the “kinetic product”, and the “1,4 product” is the thermodynamic product (i.e. has a more stable double  bond).

It seems understandable that the 1,4-product is the thermodynamic product, since it has the most substituted double bond.

But it does seem a bit weird that the 1,2-product would be kinetic. After all, we’re not dealing with a free carbocation here.

Two thoughts on this. First, it might help to think of the bromonium ion as being in equilibrium with a free carbocation. The carbon best able to stabilize this positive charge is C-2, since it is secondary and resonance-stabilized.

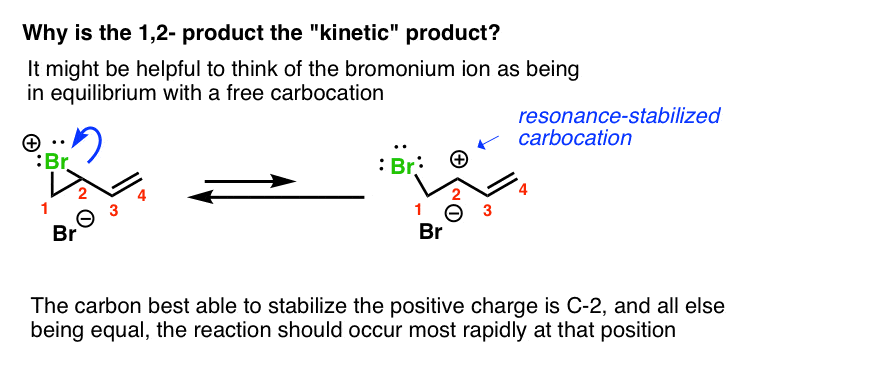
If you look at it this way, then this leads down the path of “1,2-addition resulting from attack at the carbon best able to stabilize positive charge”, as we’ve seen before.

7. A Different Rationalization For Why The 1,2- Product Is The Kinetic Product: Ion Pairing

There is a second way to look at it. The “kinetic product” could also be a result of the fact that the Br(-) forms a relatively tight ion pair with the bromonium ion. The idea here is that at low temperatures the Br(-) is held closely to the bromonium ion through electrostatic attraction, and thus will attack the closest electrophile (C-2).

So which is right? Does the 1,2-addition occur faster because the carbon is best able to stabilize positive charge, or is it faster because of ion pairing?

In this example, the “most stable carbocation” and “tight ion pair” rationalizations happen to give you the same result. Unfortunately, these rationalizations can give different results with some more complex dienes, and textbooks conflict as to which rationalization to use.

Which brings us to our practice problems.

8. Thinking Through “Kinetic” and “Thermodynamic” Control – Three Practice Problems

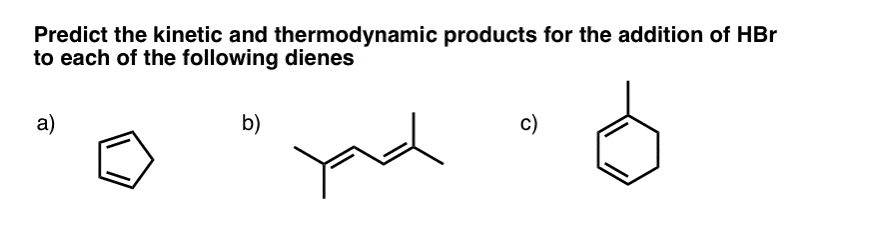
In this post and in the one previous, we’ve seen that there are two factors to consider when evaluating whether products are “kinetic” or “thermodynamic”.

• The relative stability of the carbocations in the intermediate resonance forms
• The relative stability of the double bonds in the final products

That’s it. The challenge is to

1. draw the intermediate resonance-stabilized carbocation(s), and
2. draw the products that would result from attack of a nucleophile on those resonance forms.

Let’s go through these three examples.

9. Question #1. Cyclopentadiene

The first example (cyclopentadiene) is a trick question, albeit a fairly straightforward one.  Why?

Look what happens when we protonate C-1. We obtain two identical resonance forms. This means that wherever the Br(-) attacks, it will lead to the same product.

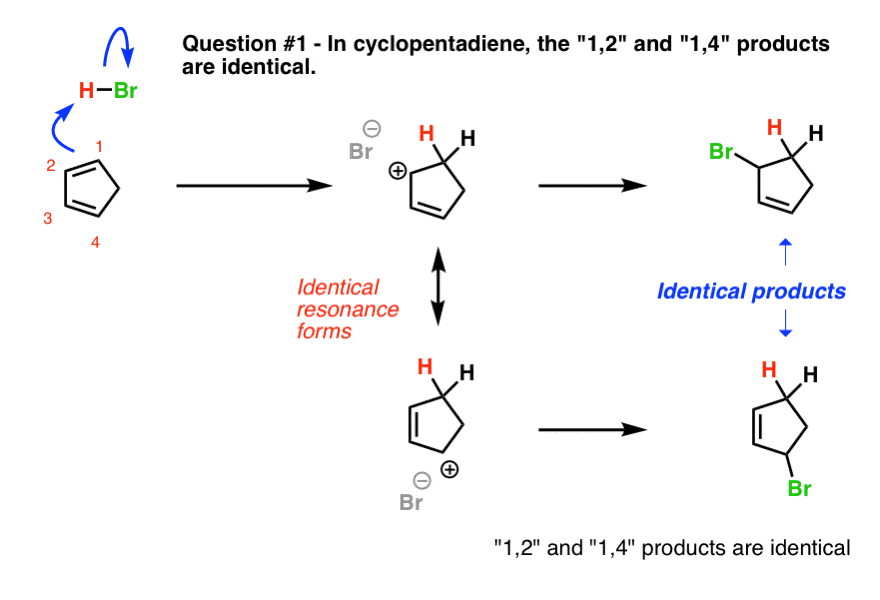
In other words, the 1,2- and 1,4- products are exactly the same!  [ Note 1]

10. Example #2 (2,5 dimethyl hexa-2-4-diene)

This is an example which can give two conflicting “correct” answers depending on which rationalization for 1,2-addition your textbook (or instructor) prefers: “carbocation stability” or “ion pairing”.  So here is some advice: if you are writing an exam on this topic,  check with your instructor and/or textbook regarding this question to see which answer they think is correct. 

(Of course, there is really only one correct answer: what do experiments tell us? But this information can be hard to find for specific examples).

Interpretation #1: The “More Stable Carbocation” Rationalization

Let’s interpret this question using the “more stable carbocation’ framework first. I happen to like this because it is good practice for applying familiar concepts in new situations.

Protonation of C-1 of 2,5-dimethyl hexa-2,4-diene results in a resonance-stabilized allylic carbocation. But look at the where the carbocation is in those two resonance forms!

The resonance form where the carbocation is on C-2 will be less important than the resonance form where the carbocation is on C-4, because C-4 is a more substituted carbon.

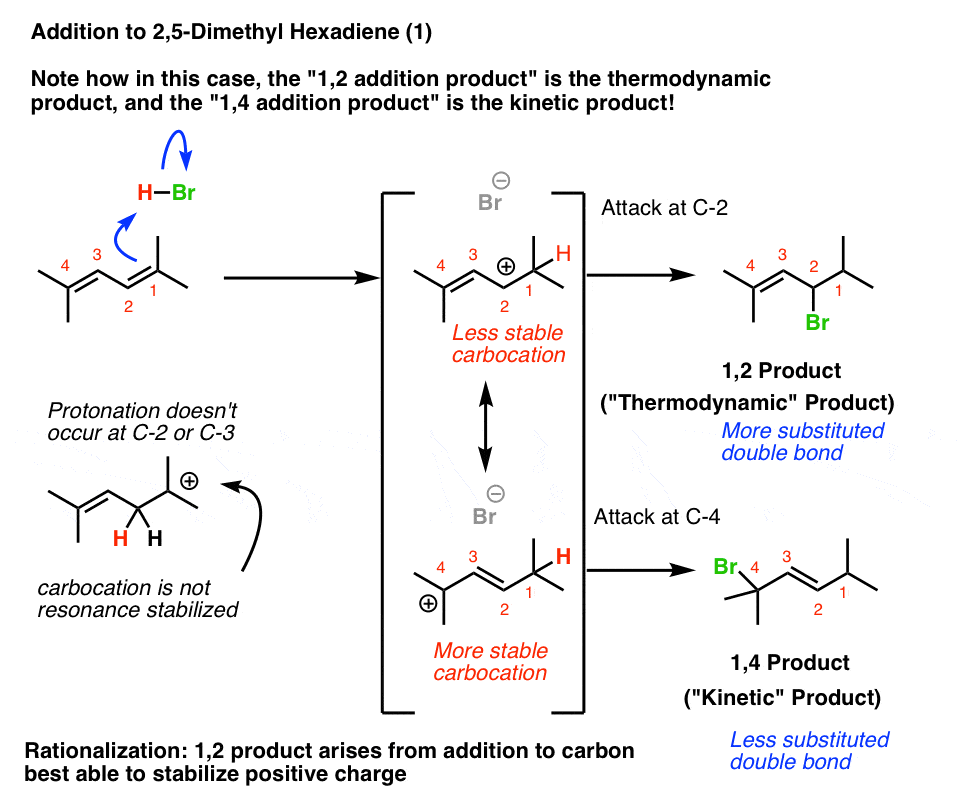
Therefore, we’d expect the 1,4-product to be the kinetic product.

Futhermore, when we look at the two possible alkene products, the 1,2-product has the more substituted (and thus more stable) double bond!

That means that the 1,2-product would be the thermodynamic product.

The bottom line here is that which product is the “kinetic product” and which product is the “thermodynamic product” depends on the structure of the starting diene. Butadiene and 2,5-dimethyl-hexa-2,4-diene give opposite results – but the principles involved are identical.

This is an example where applying concepts rather than just memorizing pays dividends. That’s also why I happen to like this problem.

Interpretation #2: The “Tight Ion Pair” Rationalization

The Loudon and Klein textbooks (and perhaps others) favor the rationalization that the 1,2-product always results at low temperatures due to ion pairing.

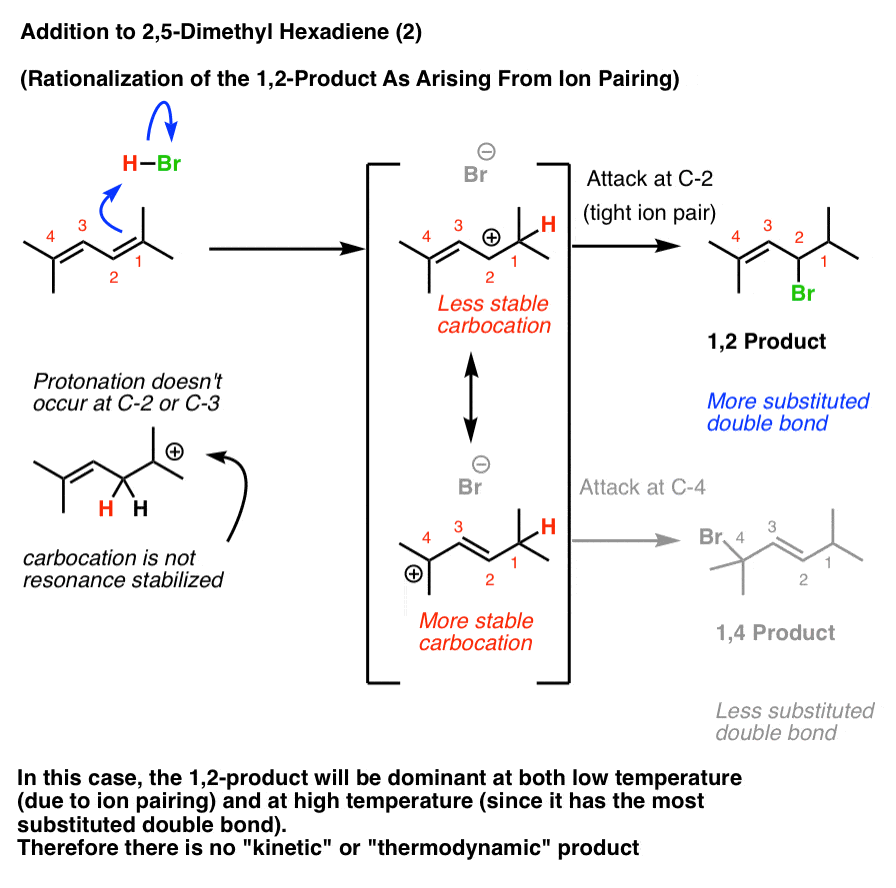
In this case, the 1,2-product will dominate both at low temperature (due to ion pairing) and higher temperature (since it has the most stable double bond). Therefore heating the reaction up to induce the reverse reaction will not change the product distribution.

[What do experiments tell us? I can’t find addition of HCl or HBr to 2,5-dimethyl hexa-2,4-diene, but  chlorination with Cl₂ gives the 1,2-product , supporting the ion-pair rationalization in that case].

11. Example #3: 1-Methyl Cyclohexadiene

Let’s look at the third (and to my mind, trickiest) example: 1-methyl cyclohexadiene.

The key to getting the right answer here hinges on choosing the most stable resonance-stabilized carbocation that can be formed through protonation.

That’s an issue because 1-methylcyclohexadiene is not symmetric!

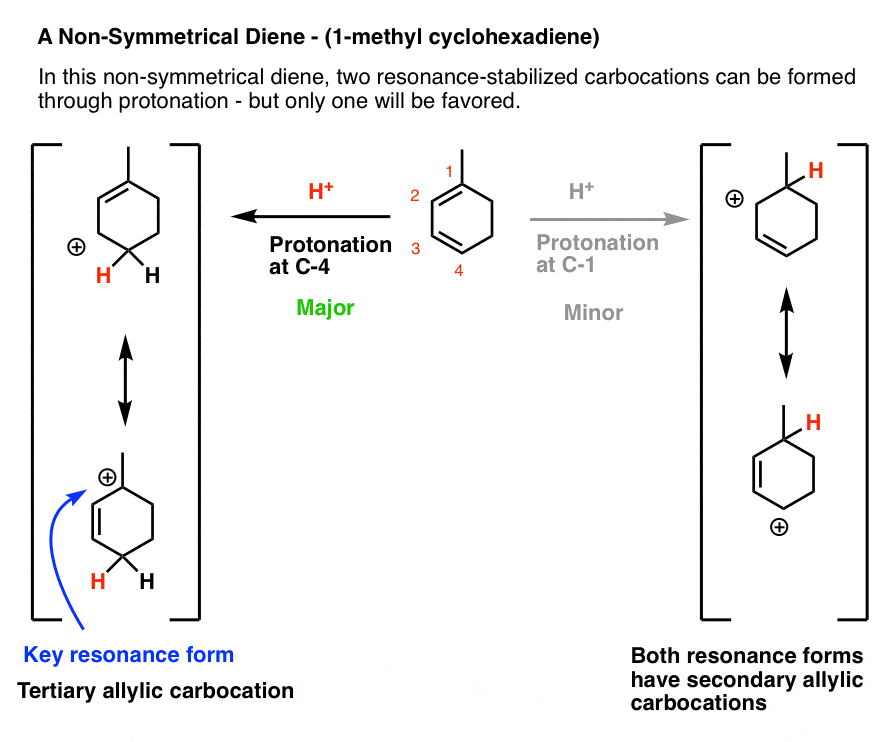
Protonation at C-1 leads to a resonance-stabilized carbocation with two resonance forms, each of which bears a secondary carbocation. That seems relatively stable, right?

However, protonation at C-4 leads to a resonance-stabilized carbocation with two resonance forms, one of which bears a secondary carbocation, and one of which bears a tertiary carbocation! This will be significantly more stable, and hence make a greater contribution to the resonance hybrid.

This means that protonation on C-4 is the best answer here. 

If we then go forward from these two resonance forms, we arrive at a situation not unlike that for 2,5-dimethyl hexa-2,4-diene, above.

If you use the “which carbon can best stabilize positive charge” rationalization, then one would expect that the 1,4 addition product would dominate at low temperature (since it would arise from attack at tertiary C-1) and 1,2-addition would be the dominant product at high temperature (since it has the most stable double bond).

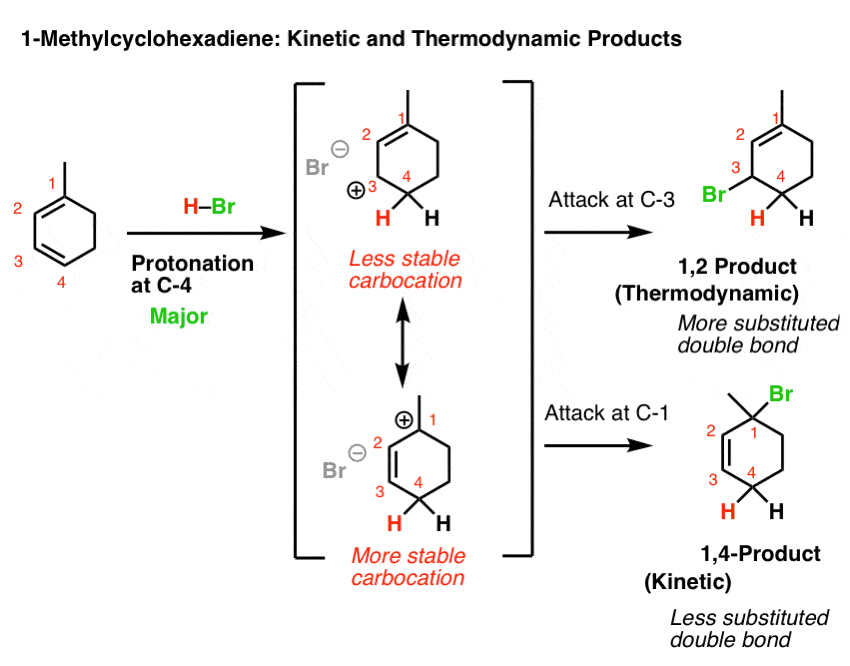
Of course, if the “ion pair” rationalization is favoured, then the 1,2-product dominates at both low and high temperatures since it has a tri-substituted double bond and the 1,4- product has a di-substituted double bond.

Again, check with your textbook/instructor to see what rationalization they use.

12. Conclusion

In summary, this is probably more than most people ever want to know or care about 1,2- versus 1,4- addition to dienes. But if you want to be prepared for an exam – and many of you reading this do! – it pays to understand the principles behind how these reactions work on a deeper level.

In the next post, we’ll transition away from polar, stepwise additions to dienes towards some relatively non-polar, concerted additions to dienes. This will set us up for discussing what is perhaps the most powerful and versatile reaction ever discovered.

Thanks to Tom Struble and Matt Pierce for helpful contributions to this post.

Notes

Note 1. This example was inspired by an exam question I once saw from an instructor/university I choose not to mention, which gave “1,4” addition as the thermodynamic product and “1,2-addition” as the kinetic product. Not kidding.

(Advanced) References and Further Reading

1. —Mobile-anion tautomerism. Part I. A preliminary study of the conditions of activation of the three-carbon system, and a discussion of the results in relation to the modes of addition to conjugated systems
   Harold Burton and Christopher Kelk Ingold
   J. Chem. Soc., 1928, 904-921
   DOI: 10.1039/JR9280000904
   One of the first papers to discuss what would later be called, “thermodynamic vs. kinetic control”. This paper discusses the addition of Br₂ to butadiene and various substituted butadienes, and how 1,2 or 1,4 addition can vary depending on substitution.
2. The modes of addition to conjugated unsaturated systems. Part IX. A discussion of mechanism and equilibrium, with a note on three-carbon prototropy
   P. B. D. de la Mare, E. D. Hughes, and C. K. Ingold
   J. Chem. Soc. 1948, 17-27
   DOI: 10.1039/JR9480000017
   This is a followup paper to Ref #1, where the authors discuss that 1,2-addition is the kinetic product of halogen addition to butadiene, and the 1,4-product is the thermodynamic product, and the kinetic product can rearrange to the thermodynamic product.
3. THE ADDITION OF HYDROGEN CHLORIDE TO BUTADIENE
   M. S. KHARASCH, J. KRITCHEVSKY, and F. R. MAYO
   The Journal of Organic Chemistry 1937, 02 (5), 489-496
   DOI: 10.1021/jo01228a010
   An early paper by University of Chicago chemist M. S. Kharasch on the addition of HCl to butadiene, seeing whether the ratio of 1,2 to 1,4 addition varied with different reaction conditions.
4. The Mechanism of Bromine Addition to 1,3-Butadiene
   Lewis F. Hatch, Pete D. Gardner, and Ronald E. Gilbert
   Journal of the American Chemical Society 1959, 81 (22), 5943-5946
   DOI: 10.1021/ja01531a025
   This is a reinvestigation of the addition of bromine to butadiene, and postulates an intermediate bromonium ion in the mechanism.
5. STUDIES OF CONJUGATED SYSTEMS. V. THE PREPARATION AND CHLORINATION OF BUTADIENE
   Irving E. Muskat and Herbert E. Northrup
   Journal of the American Chemical Society 1930, 52 (10), 4043-4055
   DOI: 10.1021/ja01373a042
   An early paper discussing not only the chlorination of butadiene, but also its synthesis. The regioselectivity is explained using “electronic formulas”, with electrophilic and nucleophilic carbons denoted by “+” and “-“ respectively.
6. Chlorination of cyclopentadiene
   Victor L. Heasley, Paul D. Davis, D. Michael Ingle, Kerry D. Rold, and Gene E. Heasley
   The Journal of Organic Chemistry 1974, 39 (5), 736-737
   DOI: 10.1021/jo00919a044
   Chlorination of cyclopentadiene gives mainly the cis-1,2-addition product.
7. Chlorination of isoprene
   E. G. E. Hawkins and M. D. Philpot
   J. Chem. Soc., 1962, 3204-3212
   DOI: 10.1039/JR9620003204
   The chlorination of isoprene largely gives the monochlorinated product (1-chloro-2-methylbutadiene) and the 1,4-addition product (1,4-dichloro-2-methylbut-2-ene).
8. THE PEROXIDE EFFECT IN THE ADDITION OF REAGENTS TO UNSATURATED COMPOUNDS. XIII. THE ADDITION OF HYDROGEN BROMIDE TO BUTADIENE
   M. S. KHARASCH, ELLY T. MARGOLIS, and FRANK R. MAYO
   The Journal of Organic Chemistry 1936, 01 (4), 393-404
   DOI: 10.1021/jo01233a008
   Another early paper by M. S. Kharasch in which he studies the addition of HBr to butadiene, in which he attempts to rigorously separate the two modes of addition – electrophilic vs. radical.
9. Regiochemistry of the addition of hydrochloric acid-d to trans-1,3-pentadiene
   J. Eric Nordlander, Philip O. Owuor, and Jerome E. Haky
   Journal of the American Chemical Society 1979 101 (5), 1288-1289
   DOI: 10.1021/ja00499a045
   Very clever experiment where DCl is added to 1,3-pentadiene, which results in a symmetrical allylic carbocation intermediate. The deuterium label allows determination of the ratio between 1,2- and 1,4- products; as it turns out, the 1,2- products predominate.
10. Solvation Dynamics and the Nature of Reaction Barriers and Ion-Pair Intermediates in Carbocation Reactions
    Vladislav A. Roytman and Daniel A. Singleton
    Journal of the American Chemical Society 2020 142 (29), 12865-12877
    DOI: 10.1021/jacs.0c06295
    1,2- vs 1,4- addition is a nice concept to teach, but this is what this very recent study has to say:
    “Additions of acids to 1,3-dienes are conventionally understood as involving discrete intermediates that undergo an ordinary competition between subsequent pathways to form the observed products. The combined experimental, computational, and dynamic trajectory study here suggests that this view is incorrect, and that solvation dynamics plays a critical role in the mechanism.”